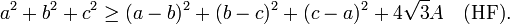Science is built up of facts, as a house is with stones.
But a collection of facts is no more a science
than a heap of stones is a house.
~Henri Poincare
The 119th day of the year; the largest amount of US money one can have in coins without being able to make change for a dollar is 119 cents. *Tanya Khovanova, Number Gossip
119 is the product of the first two primes ending with 7
119 is the sum of five consecutive primes (17 + 19 + 23 + 29 + 31).
119 is the order of the largest cyclic subgroups of the Monster group.
There are 119 prime numbers which gets displayed on a 12-hour digital clock.
119 is the smallest composite number, and the only year date, that is one less than a factorial. The next will be 40319 = 8! - 1. (students might examine the sequence of n! + 1 for patterns)
119 is a Perrin Number, A Fibonacci like sequence that begins with 3, 0, 2 and then each new value is the sum of the two digits before the last known, so it starts 3, 0, 2, 3, 2, 5, 5, 7, ... The name is for French mathematician Francois Perrin who wrote about it in 1899,
EVENTS
1657 Christiaan Huygens published De Ratiociniis in Ludo Aleae [Reasoning in games of chance] on the calculus of probabilities, the first printed work on the subject.
John Arbuthnot translated Huygens' "De ratiociniis in ludo aleae " in 1692 and extended it by adding a few further games of chance. This was the first work on probability published in English.
In 1699, the French Academy of Sciences held its first public meeting, in the Louvre. *TIS
1756 Benjamin Franklin was elected a Fellow of the Royal Society on April 29, 1756. Under the rules candidates had to be recommended in writing by three or more Fellows acquainted with him “either in person or by his Works,” the recommendation had to be approved by the Council, and the certificate publicly displayed at “ten several ordinary meetings” before balloting. Nothing more was required of foreign fellows. British (including colonial) fellows, however, had to pay an admission fee (five guineas after 1752) and a sum of £21 “for the use of the Society in lieu of Contributions,” or give bond for that amount. Only then was a British subject deemed to be a fellow and entitled to be registered in the Journal-Book and be included in the printed List of Fellows. To attend meetings and vote in elections British fellows had also to sign the obligation to “endeavor to promote the Good of the Royall Society … and to pursue the Ends for which the same was formed.” *Franklin Papers, Natl. Archives
1831 Wilhelm Eduard Weber is offered the position of full professor of Physics at Gottingen to fill the position of Tobias Mayer, partially on the recommendation of Gauss.
In December 1837, the Hanoverian government dismissed Weber, one of the Göttingen Seven(a group of seven liberal professors at University of Göttingen. In 1837, they protested against the annullment of the constitution of the Kingdom of Hanover by its new ruler, King Ernest Augustus, and refused to swear an oath to the king.), from his post at the university for political reasons. Weber then travelled for a time, visiting England, among other countries, and became professor of physics in Leipzig from 1843 to 1849, when he was reinstated at Göttingen. One of his most important works, co-authored with Carl Friedrich Gauss and Carl Wolfgang Benjamin Goldschmidt, was Atlas des Erdmagnetismus: nach den Elementen der Theorie entworfen (Atlas of Geomagnetism: Designed according to the elements of the theory), a series of magnetic maps, and it was chiefly through his efforts that magnetic observatories were instituted. He studied magnetism with Gauss, and during 1864 published his Electrodynamic Proportional Measures containing a system of absolute measurements for electric currents, which forms the basis of those in use. Weber died in Göttingen, where he is buried in the same cemetery as Max Planck and Max Born.*Wik
Together with Gauss, he invented the magnetic telegraph in 1833, which connected the observatory with the institute for physics in Göttingen.
1832 Evariste Galois released from prison. On (1831)Bastille Day, Galois was at the head of a protest, wearing the uniform of the disbanded artillery, and came heavily armed with several pistols, a rifle, and a dagger. For this, he was again arrested and this time sentenced to six months in prison for illegally wearing a uniform. He was released on April 29, 1832. During his imprisonment, he continued developing his mathematical ideas.*Wik (He will be shot on the morning of May 30, and die the next day, 1832)
The Galois memorial in the cemetery of Bourg-la-Reine. Évariste Galois was buried in a common grave and the exact location is unknown.
1854 Lincoln University, the first university for Blacks, is incorporated. Lincoln University of the Commonwealth of Pennsylvania was chartered in April 1854 as Ashmun Institute. As Horace Mann Bond, '23, the eighth president of Lincoln University, so eloquently cites in the opening chapter of his book, Education for Freedom, this was "the first institution found anywhere in the world to provide a higher education in the arts and sciences for male youth of African descent." The story of Lincoln University goes back to the early years of the 19th century and to the ancestors of its founder, John Miller Dickey, and his wife, Sarah Emlen Cresson. The Institute was re-named Lincoln University in 1866 after President Abraham Lincoln. *Lincoln University web site
Lincoln University has numerous notable alumni, including US Supreme Court Justice Thurgood Marshall; Harlem Renaissance poet Langston Hughes; Medal of Honor recipient and pioneering African-American editor Christian Fleetwood; former US Ambassador to Botswana, Horace Dawson; civil rights activist Frederick D. Alexander; the first president of Nigeria, and Nnamdi Azikiwe; the first president of Ghana
Student Union, Lincoln University.
1901 Math Blunder succeeds, "But a more recent, a veritably shocking, example is at hand. On April 29, 1901, a Mr. Israel Euclid Eabinovitch submitted to the Board of University Studies of the Johns Hopkins University, in conformity with the requirements for the degree of doctor of philosophy, a dissertation in which, after an introduction full of the most palpable blunders, he proceeds to persuade himself that he proves Euclid's parallel postulate by using the worn-out device of attacking it from space of three dimensions, a device already squeezed dry and discarded by the very creator of non-Euclidean geometry, Janos Bolyai. And his dissertation was accepted by the referees. (Science Monthly, Vol 67, page 642)


1925 The first woman, F. R. Sabin, is elected to the National Academy of Sciences (Kane, p. 945). *VFR She was a histology professor at Johns Hopkins University.
Julia Robinson was the first woman to serve as president of the American Mathematical Society, and was also the first woman mathematician to be elected to the U.S. National Academy of Sciences, in 1975.
1931 Robert Lee Moore elected to the National Academy of Sciences. *VFR
BIRTHS
1667 John Arbuthnot (baptised April 29, 1667 – February 27, 1735), fellow of the Royal College of Physicians. In 1710, his paper “An argument for divine providence taken form the constant regularity observ’s in the bith of both sexes” gave the first example of statistical inference. In his day he was famous for his political satires, from which we still know the character John Bull. *VFR
He inspired both Jonathan Swift's Gulliver's Travels book III and Alexander Pope's Peri Bathous, Or the Art of Sinking in Poetry, Memoirs of Martin Scriblerus,m (Wikipedia) He also translated Huygens' "De ratiociniis in ludo aleae " in 1692 and extended it by adding a few further games of chance. This was the first work on probability published in English.*SAU
Also known for his statistical analysis of the male and female birth rates in England. This is probably the first use of probability in a social statistical analysis and the earliest case of a statistical significance test. *RMAT
"He also contributed to the development of archaeology and history with his papers on Tables of Grecian, Roman, and Jewish measures, weights and coins; reduced to the English standard.”
Title page from my 1705, first edition copy of this publication by John Arbuthnot." *coffeefueled
 |
| *Wik |
1850 William Edward Story (April 29, 1850 in Boston, Massachusetts, U.S. - April 10, 1930 in Worcester, Massachusetts, U.S.) He taught at Johns Hopkins with Sylvester and then moved on to Clark University which was, during the early 1890’s, the strongest mathematics department in the country. In the 1890’s he edited the short lived Mathematical Reviews.*VFR
.png)
1854 Jules Henri Poincare (29 April 1854 – 17 July 1912) born in Nancy, France. He did important work in function theory, algebraic geometry, number theory, algebra, celestial mechanics, differential equations, mathematical physics, algebraic topology, and philosophy of mathematics. There may never be another universal mathematician like Poincar´e. *VFR His Poincaré Conjecture holds that if any loop in a given three-dimensional space can be shrunk to a point, the space is equivalent to a sphere. Its proof remains an unsolved problem in topology. He influenced cosmogony, relativity, and topology. In applied mathematics he also studied optics, electricity, telegraphy, capillarity, elasticity, thermodynamics, potential theory, quantum theory, and cosmology. He is often described as the last universalist in mathematics. He studied the three-body-problem in celestial mechanics, and theories of light and electromagnetic waves. He was a co-discoverer (with Albert Einstein and Hendrik Lorentz) of the special theory of relativity. *TIS

1872 Forest Ray Moulton (29 Apr 1872 (in a log cabin near the small town of Leroy, Michigan); 7 Dec 1952 at age 80) American astronomer who collaborated with Thomas Chamberlin in advancing the planetesimal theory of the origin of the solar system (1904). They suggested filaments of matter were ejected when a star passed close to the Sun, which cooled into tiny solid fragments, “planetesimals.” Over a very long period, grains collided and stuck together. Continued accretion created pebbles, boulders, and eventually larger bodies whose gravitational force of attraction accelerated the formation of protoplanets. (This formation by accretion is still accepted, but not the stellar origin of the planetesimals.) Moulton was first to suggest that the smaller satellites of Jupiter discovered by Nicholson and others in the early 20th century were captured asteroids, now widely accepted. *TIS

1894 Marietta Blau (29 April 1894 – 27 January 1970) was an Austrian physicist credited with developing photographic nuclear emulsions that were usefully able to image and accurately measure high-energy nuclear particles and events, significantly advancing the field of particle physics in her time. For this, she was awarded the Lieben Prize by the Austrian Academy of Sciences. As a Jew, she was forced to flee Austria when Nazi Germany annexed it in 1938, eventually making her way to the United States. She was nominated for Nobel Prizes in both physics and chemistry for her work, but did not win. After her return to Austria, she won the Erwin Schrödinger Prize from the Austrian Academy of Sciences. *Wik
Austrian nuclear physicist who began as a strong student in mathematics and physics at school, and studied physics at university, where she wrote her thesis on the absorption of gamma rays (1919). At first, she took a job (1921) with a manufacturer of x-ray tubes in Berlin. By 1923, she progressed to researching radioactivity with the Institut für Radiumforschung back in Vienna. There she developed the photographic emulsion technique for the study of nuclear disintegration caused by cosmic rays, and contributed to development of photomultiplier tubes. Blau was first to use nuclear emulsions to detect neutrons by observing recoil protons. Albert Einstein recognized her as a very capable experimental physicist, and after 1938 when she fled the rise of the Nazis, Einstein helped her career continue in Mexico City and then the U.S. *TIS

1906 Eugène Ehrhart (29 April 1906 Guebwiller – 17 January 2000 Strasbourg) was a French mathematician who introduced Ehrhart polynomials in the 1960s. Ehrhart received his high school diploma at the age of 22. He was a mathematics teacher in several high schools, and did mathematics research on his own time. He started publishing in mathematics in his 40s, and finished his PhD thesis at the age of 60. The theory of Ehrhart polynomials can be seen as a higher-dimensional generalization of Pick's theorem. *Wik

1926 Vera Nikolaevna Maslennikova (29 April 1926, Priluki, Russia - 14 August 2000) Gelfond supervised her diploma work at Moscow and Sobolev directed her Ph.D. at the Steklov Mathematical Institute. She has published more than 80 papers in the theory of partial differential equations, the mathematical hydrodynamics of rotating fluids, and in function spaces.*VFR She has worked in the field of partial differential equations, the mathematical hydrodynamics of rotating fluids, and in function spaces, having published more than one hundred and forty research papers. *Wik
1928 Laszlo Belady,( April 29, 1928 in Budapest - November 6, 2021) creator of the Belady algorithm (used in optimizing the performance of computers), is born. Belady worked at IBM for 23 years in software engineering before joining the Mitsubishi Electronics Research Laboratory in the mid-1980s. He wins numerous awards, including the J.D. Warnier Prize for Excellence in Information and an IEEE fellowship. *CHM

1930 Yuan Wang (29 April 1930 in Lanhsi, Zhejiang province, China - 14 May 2021) )Most of Wang Yuan's research has been in the area of number theory. He looked at sieve methods and applied them to the Goldbach Conjecture. He also applied circle methods to the Goldbach Conjecture. In 1956 he published (in Chinese) On the representation of large even integer as a sum of a prime and a product of at most 4 primes in which he assumed the truth of the Riemann hypothesis and with that assumption proved that every large even integer is the sum of a prime and of a product of at most 4 primes. He also proved that there are infinitely many primes p such that p + 2 is a product of at most 4 primes. In 1957 Wang Yuan published four papers: On sieve methods and some of their applications; On some properties of integral valued polynomials; On the representation of large even number as a sum of two almost-primes; and On sieve methods and some of the related problems.*SAU

1936 Volker Strassen (April 29, 1936 - ) is a German mathematician, a professor emeritus in the department of mathematics and statistics at the University of Konstanz. Strassen began his researches as a probabilist; his 1964 paper An Invariance Principle for the Law of the Iterated Logarithm defined a functional form of the law of the iterated logarithm, showing a form of scale invariance in random walks. This result, now known as Strassen's invariance principle or as Strassen's law of the iterated logarithm, has been highly cited and led to a 1966 presentation at the International Congress of Mathematicians.
In 1969, Strassen shifted his research efforts towards the analysis of algorithms with a paper on Gaussian elimination, introducing Strassen's algorithm, the first algorithm for performing matrix multiplication faster than the O(n3) time bound that would result from a naive algorithm. In the same paper he also presented an asymptotically-fast algorithm to perform matrix inversion, based on the fast matrix multiplication algorithm. This result was an important theoretical breakthrough, leading to much additional research on fast matrix multiplication, and despite later theoretical improvements it remains a practical method for multiplication of dense matrices of moderate to large sizes. In 1971 Strassen published another paper together with Arnold Schönhage on asymptotically-fast integer multiplication based on the fast Fourier transform; see the Schönhage–Strassen algorithm. Strassen is also known for his 1977 work with Robert M. Solovay on the Solovay–Strassen primality test, the first method to show that testing whether a number is prime can be performed in randomized polynomial time and one of the first results to show the power of randomized algorithms more generally.*Wik

DEATHS
1633 Francis Godwin, an English cleric, was buried Apr. 29, 1633, at about age 71. As Bishop of Hereford, Godwin published a number of mainstream theological tracts, but he left behind at his death a manuscript about a fantasy voyage undertaken by a Spaniard, Domingo Gonsales. While at the island of St. Helena, Gonsales had discovered a species of wild swans, which he called “gansa” and which he discovered could be trained to fly in harness and carry a load. He rigged up an aerial chariot, hooked 25 gansas to it, and off he flew on a brief test flight. He was picked up on St. Helena by a ship from the Indies, and he persuaded the captain to make room for the swans and the chariot. When the ship was attacked by pirates off the Canaries, Gonsales climbed in his gondola, hooked up the gansas, and escaped. But the gansas had minds of their own, and kept flying up and up, until they ultimately escaped the force of the earth’s gravity (an interesting notion, because in 1630, no one believed in a force of gravity). Eventually, they reached the Moon, where Gonsales discovered that the Moon is inhabited by a race of peaceful giants, who swooned when they heard the name “Jesus” and converted instantly to Christianity.
It was a wonderful tale, and it could have been buried with the bishop, but it was salvaged and published in 1638 as The Man in the Moone: or, A Discourse of a Voyage Thither, with a wonderful frontispiece showing Gonsales in his gansa-powered flying machine. This first edition is very scarce (four known copies), but it was republished in 1657, and also translated into French in 1648; we were very fortunate to acquire a 1666 edition of the French translation just last year. It includes the charming illustration of the “little goose coupe”, as well as a depiction of the language of the Lunarians, which is sung without words (the second tune is lunar for “Gonsales”).
If you look closely at the publication date, you have the rare chance to see the first 7 Roman numerals in ascending order, starting from the right. This is one of the reasons why the year 1666 was feared as an annus mirabilis by the English, a fear not disproved by the arrival of the bubonic plaque and the Great Fire of London. *LH

1713 Francis Hauksbee the elder (baptized on 27 May 1660 in Colchester–buried in St Dunstan's-in-the-West, London on 29 April 1713.), also known as Francis Hawksbee, was an 18th-century English scientist best known for his work on electricity and electrostatic repulsion.
Initially apprenticed in 1678 to his elder brother as a draper, Hauksbee became Isaac Newton’s lab assistant. In 1703 he was appointed curator, instrument maker and experimentalist of the Royal Society by Newton, who had recently become president of the society and wished to resurrect the Royal Society’s weekly demonstrations.
Until 1705, most of these experiments were air pump experiments of a mundane nature, but Hauksbee then turned to investigating the luminosity of mercury which was known to emit a glow under barometric vacuum conditions.
By 1705, Hauksbee had discovered that if he placed a small amount of mercury in the glass of his modified version of Otto von Guericke's generator, evacuated the air from it to create a mild vacuum and rubbed the ball in order to build up a charge, a glow was visible if he placed his hand on the outside of the ball. This glow was bright enough to read by. It seemed to be similar to St. Elmo's Fire. This effect later became the basis of the gas-discharge lamp, which led to neon lighting and mercury vapor lamps. In 1706 he produced an 'Influence machine' to generate this effect. He was elected a Fellow of the Royal Society the same year.

Hauksbee continued to experiment with electricity, making numerous observations and developing machines to generate and demonstrate various electrical phenomena. In 1709 he published Physico-Mechanical Experiments on Various Subjects which summarized much of his scientific work.
In 1708, Hauksbee independently discovered Charles' law of gases, which states that, for a given mass of gas at a constant pressure, the volume of the gas is proportional to its temperature.
The Royal Society Hauksbee Awards, awarded in 2010, were given by the Royal Society to the “unsung heroes of science, technology, engineering and mathematics.” *Wik
1862 John Edward Campbell (27 May 1862, Lisburn, Ireland – 1 October 1924, Oxford, Oxfordshire, England) is remembered for the Campbell-Baker-Hausdorff theorem which gives a formula for multiplication of exponentials in Lie algebras. *SAU His 1903 book, Introductory Treatise on Lie's Theory of Finite Continuous Transformation Groups, popularized the ideas of Sophus Lie among British mathematicians.
He was elected a Fellow of the Royal Society in 1905, and served as President of the London Mathematical Society from 1918 to 1920. *Wik *Renaissance Mathematicus


1864 Charles-Julien Brianchon (19 Dec 1783, 29 Apr 1864 at age 80) French mathematician who published a geometrical theorem (named as Brianchon's theorem) while a student (1806). He showed that in any hexagon formed of six tangents to a conic, the three diagonals meet at a point. (Conics include circles, ellipses, parabolas, and hyperbolas.) In fact, this theorem is simply the dual of Pascal's theorem which was proved in 1639. After graduation, Brianchon became a lieutenant in artillery fighting in Napoleon's army until he left active service in 1813 due to ill health. His last work in mathematics made the first use of the term "nine-point circle." By 1823, Brianchon's interests turned to teaching and to chemistry. *TIS
1872 Jean-Marie-Constant Duhamel (5 Feb 1797, 29 Apr 1872 at age 75) French mathematician and physicist who proposed a theory dealing with the transmission of heat in crystal structures based on the work of the French mathematicians Jean-Baptiste-Joseph Fourier and Siméon-Denis Poisson. *TIS
1894 Giuseppe Battaglini (11 Jan 1826 in Naples, Kingdom of Naples and Sicily (now Italy) - 29 Apr 1894 in Naples, Italy ) Some of Battaglini's results have proved significant. For example, in his doctoral dissertation of 1868, Klein introduced a classification scheme for second-degree line complexes based on Battaglini's earlier work. However, his main importance is his modern approach to mathematics which played a major role in invigorating the Italian university system, particularly in his efforts to bring the non-Euclidean geometry of Lobachevsky and Bolyai to the Italian speaking world. Jules Hoüel played a similar role for non-Euclidean geometry in the French speaking world and the correspondence between the two (see [6]) provides a vivid picture of the reactions of both the French and the Italian mathematical communities against the non-Euclidean geometries. Battaglini and Hoüel also exchanged ideas relating to mathematical education in various European countries. In particular they debated the use of Euclid's Elements as a textbook for teaching elementary geometry in schools. *SAU

1916 – Jørgen Pedersen Gram (June 27, 1850 – April 29, 1916) was a Danish actuary and mathematician who was born in Nustrup, Duchy of Schleswig, Denmark and died in Copenhagen, Denmark.
Important papers of his include On series expansions determined by the methods of least squares, and Investigations of the number of primes less than a given number. The mathematical method that bears his name, the Gram–Schmidt process, was first published in the former paper, in 1883. The Gramian matrix is also named after him.
For number theorists his main fame is the series for the Riemann zeta function (the leading function in Riemann's exact prime-counting function). Instead of using a series of logarithmic integrals, Gram's function uses logarithm powers and the zeta function of positive integers. It has recently been supplanted by a formula of Ramanujan that uses the Bernoulli numbers directly instead of the zeta function.
Gram was the first mathematician to provide a systematic theory of the development of skew frequency curves, showing that the normal symmetric Gaussian error curve was but one special case of a more general class of frequency curves.
He died after being struck by a bicycle.*Wik

1951 Ludwig Josef Johann Wittgenstein (26 April 1889 – 29 April 1951) was an Austrian-British philosopher who worked primarily in logic, the philosophy of mathematics, the philosophy of mind, and the philosophy of language. He was professor in philosophy at the University of Cambridge from 1939 until 1947. In his lifetime he published just one book review, one article, a children's dictionary, and the 75-page Tractatus Logico-Philosophicus (1921). In 1999 his posthumously published Philosophical Investigations (1953) was ranked as the most important book of 20th-century philosophy, standing out as "...the one crossover masterpiece in twentieth-century philosophy, appealing across diverse specializations and philosophical orientations". Bertrand Russell described him as "the most perfect example I have ever known of genius as traditionally conceived, passionate, profound, intense, and dominating". *Wik He died three days after his birthday. He is buried in a cemetery off Huntington Road in Cambridge, UK.

1966 William Henry Eccles FRS (23 August 1875 – 29 April 1966) British physicist who pioneered in the development of radio communication. He was an early proponent of Oliver Heaviside's theory that an upper layer of the atmosphere reflects radio waves, thus enabling their transmission over long distances. He also suggested in 1912 that solar radiation accounted for the differences in wave propagation during the day and night. He experimented with detectors and amplifiers for radio reception, coined the term "diode," and studied atmospheric disturbances of radio reception. After WW I, he made many contributions to electronic circuit development, including the Eccles-Jordan "flip-flop" patented in 1918 and used in binary counters (working with F.W. Jordan).* *TIS
.jpg)
1970 Paul Finsler (born 11 April 1894, in Heilbronn, Germany,- 29 April 1970 in Zurich, Switzerland)Finsler did his undergraduate studies at the Technische Hochschule Stuttgart, and his graduate studies at the University of Göttingen, where he received his Ph.D. in 1919 under the supervision of Constantin Carathéodory. He joined the faculty of the University of Zurich in 1927, and was promoted to ordinary professor there in 1944.
Finsler's thesis work concerned differential geometry, and Finsler spaces were named after him by Élie Cartan in 1934. The Hadwiger–Finsler inequality, a relation between the side lengths and area of a triangle in the Euclidean plane, is named after Finsler and his co-author Hugo Hadwiger. Finsler is also known for his work on the foundations of mathematics, developing a non-well-founded set theory with which he hoped to resolve the contradictions implied by Russell's paradox.
In mathematics, the Hadwiger–Finsler inequality is a result on the geometry of triangles in the Euclidean plane, named after the mathematicians Hugo Hadwiger and Paul Finsler. It states that if a triangle in the plane has side lengths a, b and c and area A, then
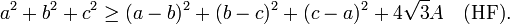
Weitzenböck's inequality is a straightforward corollary of the Hadwiger–Finsler inequality: if a triangle in the plane has side lengths a, b and c and area A, then

Weitzenböck's inequality can also be proved using Heron's formula, by which route it can be seen that equality holds in (W) if and only if the triangle is an equilateral triangle, i.e. a = b = c.
*Wik
2008 Mary Golda Ross (August 9, 1908 – April 29, 2008) was the first known Native American female engineer, and the first female engineer in the history of Lockheed. She was one of the 40 founding engineers of the renowned and highly secretive Skunk Works project at Lockheed Corporation. She worked at Lockheed from 1942 until her retirement in 1973, where she was best remembered for her work on aerospace design – including the Agena Rocket program – as well as numerous "design concepts for interplanetary space travel, crewed and uncrewed Earth-orbiting flights, the earliest studies of orbiting satellites for both defense and civilian purposes." In 2018, she was chosen to be depicted on the 2019 Native American $1 Coin by the U.S. Mint celebrating American Indians in the space program. *Wik
Credits :
*CHM=Computer History Museum
*FFF=Kane, Famous First Facts
*NSEC= NASA Solar Eclipse Calendar
*RMAT= The Renaissance Mathematicus, Thony Christie
*SAU=St Andrews Univ. Math History
*TIA = Today in Astronomy
*TIS= Today in Science History
*VFR = V Frederick Rickey, USMA
*Wik = Wikipedia
*WM = Women of Mathematics, Grinstein & Campbell












.png)















.jpg)